VŨ TRỤ HỌC
CỦA
PYTHAGORAS VÀ TRƯỜNG PHÁI
(1967)

Tác giả: James Andrew Coleman* 
Người dịch: Nguyễn Văn Khoa

*

Để độc giả có thể theo dõi dễ dàng và lý thú hơn trích đoạn, chúng tôi đã thêm vào bản dịch dưới đây một số tiểu tựa không có trong nguyên bản.  

*

Pythagoras và những người kế nghiệp ông trong trường phái do ông thành lập đã giữ một vai trò quan trọng trong lịch sử phát triển của vũ trụ học và các lý thuyết về nguồn gốc vũ trụ. Bản thân Pythagoras sống trong khoảng thời gian từ năm 580 đến 500 tCn. Ông sinh ra ở Samos (vùng Ionia*), nhưng di cư đến Kroton (ở miền nam nước Ý) vào khoảng năm 530 tCn, và dựng lên tại đây  một trường phái được gọi theo tên ông, chủ yếu là một giáo phái và triết phái mật truyền. Ảnh hưởng của Pythagoras đối với khoa học và học thuật là rất lớn: theo một ký truyền, sau bài thuyết giảng đầu tiên của ông trước dân Kroton, ông đã tạo được sự kính trọng của họ tới mức là khoảng 600 người đã tự nguyện theo ông để sống và học mà không cả về nhà từ biệt gia đình!

1 - Nguyên tố của vũ trụ: các con số và công thức toán học

Pythagoras cũng tin như các triết gia Hy Lạp trước ông, rằng có một thể chất cơ bản ở khắp nơi trong vũ trụ. Nhưng đối với ông và học trò thì thực thể đó không phải là vật chất mà thuần túy là những con số và công thức toán học; chính chúng mới là chất thể cơ bản làm nền tảng cho mọi vật trong vũ trụ – tất cả các khía cạnh vật chất, hình thức, cấu trúc và định luật cai quản mọi chuyển động của nó. Nếu con người hiểu những con số và biết suy luận, hắn sẽ hiểu thấu mọi bí ẩn của vũ trụ. Vì vậy, đối với trường phái Pythagoras, việc nghiên cứu các con số là nỗ lực cao quý nhất mà con người có thể thực hiện.

Trên thực tế, con số còn có ý nghĩa to lớn hơn là một kỹ xảo có thể tách rời khỏi vũ trụ vật chất nhằm đạt được những giải thích cho mọi cơ chế vận động của nó. Đối với Pythagoras và học trò, con số là tinh thể tối cao của sự tồn tại mà nó là hiện thân, hoàn toàn tách biệt với vật chất, và do đó, với thế giới thấp hơn của những giác quan. Thông qua con số, con người có thể tìm thấy chân lý cuối cùng và vô nhiễm, do hắn không còn bị cản trở bởi những đam mê và ham muốn của nhân thân. Họ đã cố gắng quy giản mọi thứ, bao gồm cả cảm xúc của con người, thành những con số và các công thức toán học, rồi gán những đặc điểm khác biệt cho các con số khác nhau.

2 - «Nhạc điệu của các thiên cầu»

Sự ưu ái những con số của trường phái Pythagoras đã tạo cơ sở cho việc mô tả các tầng trời thông qua cái mà họ gọi là «nhạc điệu của các thiên cầu». Điều này thể hiện sự mở rộng các quy luật cơ bản của sự hài hòa âm nhạc tới những chuyển động của các thiên thể. Pythagoras đã khám phá ra các định luật cơ bản của những dây rung và biết rằng sự hài hòa dễ chịu nhất xảy ra giữa hai dây rung khi tỷ số các tần số của chúng gần với một số nguyên nhất tới mức có thể. Ví dụ, hai dây rung có tần số với tỷ lệ 2:1 là dễ chịu nhất; tiếp theo sẽ là các tần số với tỷ lệ 3:2; tiếp theo nữa là  với tỷ lệ 4:3, v. v… Ý tưởng này dẫn đến việc thiết lập một âm giai tám âm với tỷ lệ nói ở trên là quãng tám, quãng năm và quãng bốn của thang âm. Vì vậy, con số tám được gọi là tình bạn, bởi vì nó biểu trưng cho sự hòa hợp hoàn hảo nhất.

Mặt Trời, Mặt Trăng và các hành tinh cũng được cho là thể hiện sự hài hòa hoàn hảo này trong những chuyển động của chúng qua các tầng trời*. Tin rằng cái quy luật hài hòa tìm thấy nơi các dây rung chỉ là một ứng dụng của quy luật phổ quát trong vũ trụ, Pythagoras và học trò đẩy ý tưởng này tới niềm tin rằng, trên đường di chuyển của chúng, mọi thiên thể đều quay [quanh Trái Đất] với các khoảng cách theo cùng tỷ lệ với các khoảng cách trên  thang âm nhạc. Họ giả định rằng Mặt Trăng có khoảng cách gần Trái Đất nhất, Mặt Trời có khoảng cách gấp đôi, Sao Kim gấp ba, Sao Thủy gấp bốn lần khoảng cách này, và phần còn lại của các hành tinh cũng theo các tỷ lệ liên tiếp tương tự.

Thật vậy, toàn bộ hệ mặt trời được coi như một quy mô âm nhạc vũ trụ khổng lồ liên tục rung ngân bởi những chuyển động của các hành tinh trên đường di chuyển của chúng. Cứ như thể toàn bộ thiên cầu là một chiếc đàn lia khổng lồ mà số dây đàn là những lộ trình của số thiên thể, thế nên khi các hành tinh di chuyển, chúng đã gây ra những dao động khiến các dây đàn rung ngân, hợp âm thành một thứ «nhạc điệu của các thiên cầu». Trên quy mô thiên cầu này, quãng cách từ Trái Đất tới Mặt Trăng là một cung; từ Mặt Trăng đến Sao Thủy là nửa cung; từ Sao Thủy tới Sao Kim là nửa cung; từ Sao Kim đến Mặt Trời là một quãng ba thứ; từ Mặt Trời tới Sao Hỏa là một cung; từ Sao Hỏa đến Sao Mộc là nửa cung; từ Sao Mộc tới Sao Thổ là nửa cung; và từ Sao Thổ đến mặt cầu của vòng sao cố định là một một quãng ba thứ.

Thứ âm nhạc của các thiên cầu này được cho là kết quả của một hệ thống âm nhạc vũ trụ, nó thực sự tạo ra những âm giai thuần túy mà tai người có thể nghe được như các cung bậc từ đàn lia hoặc bất kỳ nhạc cụ nào khác. Và vì Mặt Trời, Mặt Trăng và các hành tinh đều được biết là rất lớn so với các vật thể trên mặt đất, nên các dao động của chúng phải tạo ra một thứ âm nhạc vang to. Do đó, nhiều lý do khác nhau đã được đưa ra nhằm giải thích vì sao con người lại không nghe thấy những giai điệu của các thiên cầu này; một trong số các giải thích đó là vì thứ âm thanh ấy đã ở với chúng ta suốt từ khi ta sinh ra mà lại không hề có một lúc im lặng tương phản nào khiến cho sự hiện diện của nó bị tiết lộ.

3 - Trái Đất và hình tròn

Đóng góp chính của Pythagoras cho thiên văn học và sự phát triển của vũ trụ học là sự kiện ông hay/và những môn đồ của ông đã khám phá ra rằng Trái Đất có hình tròn. Các bằng chứng được họ đưa ra phần nào thuộc lĩnh vực triết học. Cơ sở của họ là niềm tin của Pythagoras và học trò rằng hình tròn là hình dạng hoàn hảo nhất, và từ đó, sự kỳ vọng rằng toàn thể vũ trụ, các thiên thể và đường di chuyển của chúng cũng hoặc sẽ có hình cầu, hoặc sẽ  chuyển động theo đường tròn.

Bằng chứng tốt nhất cho sự kiện Trái Đất có hình tròn theo quan điểm vật lý là, trong một kỳ nguyệt thực, chúng ta quan sát thấy cái bóng của Trái Đất trên Mặt Trăng là hình tròn. Các lý do khác được đưa ra là: 1) phần dưới của một con tàu bị che khuất khi nó di chuyển dọc theo đường chân trời, và 2) các vì sao có vẻ như dâng cao lên hoặc hạ thấp xuống trên bầu trời, khi ta di chuyển lên phía Bắc hoặc xuống phía Nam [bán cầu].

Khái niệm về hình tròn như một đặc trưng cơ bản của tự nhiên đã được Pythagoras và các môn đồ đưa vào quan điểm của họ về vũ trụ học. Trái Đất nằm ở trung tâm vũ trụ; Mặt Trời, Mặt Trăng, các hành tinh, và các vì sao, được quan niệm như gắn vào các vòng tròn xa gần khác nhau, đều quay chung quanh nó. Thứ tự mà họ đưa ra, bên ngoài Trái Đất, lần lượt là Mặt Trăng, Sao Thủy, Sao Kim, Mặt Trời, Sao Hỏa, Sao Mộc, Sao Thổ và các vì sao cố định (xem minh họa ở bài: James A. Coleman, Toán Học Và Thiên Văn Học ở Babylonia Và Ai Cập trên cùng trang mục này).

4 – Đối thể của Trái Đất - Chuyển động quay của Trái Đất

Về sau, những người theo trường phái Pythagoras còn phác họa vị trí của Trái Đất so với các thiên thể khác trong một bức tranh vật lý theo đó Trái Đất là một cơ thể xoay quanh một khối lửa nằm ở trung tâm vũ trụ. Lửa được đặt ở vị trí trung tâm vì nó được cho là cao quý hơn đất, và do đó được trao cho vị trí danh dự này. Những người theo chủ thuyết Pythagoras đời sau còn phát minh ra một đối thể của Trái Đất (counter-Earth), đối thể này cũng xoay quanh khối lửa trung tâm, nhưng do bị khối lửa đó che giấu nên vẫn là vô hình đối với chúng ta trên mặt đất. Không tư liệu còn tồn tại nào cho biết cái lý do đã khiến họ giả định một đối thể cho Trái Đất, nhưng một số giải thích đã được nghĩ tới. Một trong số đó là, do sự kiện số kỳ nguyệt thực xảy ra được quan sát thấy nhiều hơn so với số lần nhật thực, nên họ mới phỏng đoán rằng một đối thể của Trái Đất có thể là cái nguyên nhân đã tạo thêm các kỳ nguyệt thực bổ sung ấy.

Một giải thích thú vị về nguồn gốc đối thể của Trái Đất đã được Aristotelēs – nhà triết học Hy Lạp vĩ đại sống sau Pythagoras khoảng 200 năm, và là người từng ghi lại nhiều thuyết giảng của các triết gia Hy Lạp cổ đại – đưa ra. Theo Aristotelēs, con số 10 được những người theo chủ thuyết Pythagoras cho là hoàn hảo và bao hàm toàn thể tinh chất của mọi con số. Do đó, số lượng những cơ thể  chuyển động trên các tầng trời phải là 10, và do chỉ mới có 9 cơ thể được biết tới vào thời Pythagoras (Trái Đất, Mặt Trời, Mặt Trăng, năm hành tinh, và vòng cầu mang các vì sao cố định), nên đối thể của Trái Đất đã được quan niệm bổ sung, để mô hình của vũ trụ trở nên hoàn hảo.

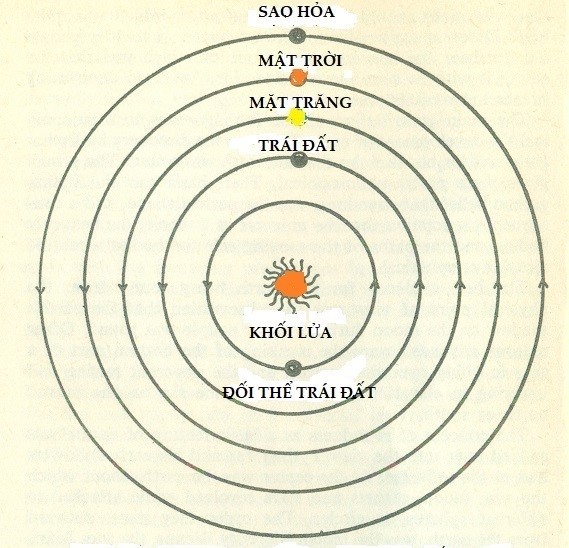
Mô hình Vũ trụ
theo các môn đồ của Pythagoras thế hệ sau

Các thành viên đời sau của trường phái Pythagoras, vào cuối thế kỷ thứ V hay đầu thế kỷ thứ IV tCn, còn đề xuất một bức tranh hoàn toàn khác về vũ trụ, giải thích chuyển động quay biểu kiến hàng ngày của thiên cầu bằng chuyển động quay của chính Trái Đất quanh cái trục của nó. Họ tuyên bố rằng mọi thứ trên trời cao kia là luôn luôn cố định và đứng yên, rằng chẳng có gì trong vũ trụ chuyển động ngoại trừ Trái Đất, rằng đây là một chuyển động quay chung quanh tâm điểm của nó, giống như một bánh xe cố định quay trên một trục từ Tây sang Đông.

James A. Coleman,
Các Học Thuyết Xưa Sớm Về Vũ Trụ
(Early Theories of The Universe,
The Pythagoreans,
Signet Science Library Book, 1967, tr. 23-26).