|
LM : 15-01-2023 |
C1 |
ĐÓNG GÓP CỦA THALĒS CHO TOÁN HỌC (1976)
Tác giả : L. N. Bunt, Ph. S. Jones, J. D. Bedient,
Người dịch : Nguyễn Văn Khoa
*
Trung tâm sớm nhất của nền văn minh Hy Lạp thực sự nằm ở các thuộc địa (Milētos, Ephesos) trên bờ biển phía tây của Tiểu Á, nơi nó đã phát triển nhanh hơn tại quê hương chính địa. Ilias và Odysseia có nguồn gốc từ đây. Khoảng 600 năm tCn, các thuộc địa Hy Lạp này rất thịnh vượng. Thương mại và đi biển là hai sinh kế quan trọng nhất. Các thuộc địa có quan hệ với Babylon (bằng đường bộ) và với Ai Cập (bằng đường biển). Hàng hải học và thiên văn học có tầm quan trọng rất lớn. Thuyền phải được đóng, nhờ vậy công nghiệp đã phát triển mạnh.
Thông qua các chuyến đi của họ, người di dân Hy Lạp đã làm quen với các môn học họ chưa từng biết trước đấy. Điều đáng chú ý là người Hy Lạp đã thể hiện một thứ quan tâm mới đối với chúng ngay từ đầu. Họ quan tâm đến các vấn đề về cái «như thế nào» và cái «tại sao» của mọi vật, chứ không chủ yếu tới những ứng dụng thực tế trước tiên. Người đặt những bước đầu tiên trên con đường đến với khoa học hiện đại của chúng ta là Thalēs xứ Milētos (624-547 tCn), được biết tới như một trong bảy «hiền giả». Thalēs là một thương gia, người ta nói rằng ông đã đi nhiều nơi và sống một thời gian dài ở Ai Cập và Babylon.
Ở Ai Cập, Thalēs từng làm vua Amasis kinh ngạc khi xác định chiều cao của một kim tự tháp từ độ dài cái bóng của nó. Theo một câu chuyện, ông ta cắm một cây gậy thẳng đứng xuống đất, và đợi cho đến khi chiều dài của cây gậy và cái bóng của nó bằng nhau; khi đó chiều cao của kim tự tháp cũng bằng với chiều dài cái bóng của nó, nên có thể đo được. Người ta cũng nói rằng ông đã dự đoán một lần nhật thực, và ông đã làm được điều này trên cơ sở những hiểu biết ông học được từ người Babylon. Theo những bức thư từ các nhà chiêm tinh của triều đình Assyria, người Babylon đã bận rộn với việc dự đoán nhật thực và nguyệt thực ngay từ khoảng năm 700 tCn. Mặc dù có lẽ những câu chuyện về Thalēs này phải được coi là huyền thoại, chúng vẫn làm rạng danh ông, và rọi sáng những quan tâm khoa học-toán học trong thời đại của ông.
Tầm quan trọng của Thalēs đối với toán học chủ yếu nằm ở chỗ ông đã tìm kiếm nền tảng lô-gic của các định lý hình học. Ông chưa từng tạo ra một hệ thống đầy đủ các định lý và chứng minh như chúng ta biết ngày nay, nhưng ông là người đầu tiên đã mạo hiểm đi theo hướng này. Các định lý ông từng suy ngẫm là khá đơn giản. Theo giả định của những tác giả đời sau, chúng là năm định lý sau:
1. Các góc ở đáy của một tam giác cân là bằng nhau.
2. Nếu hai đường thẳng cắt nhau thì các góc đối đỉnh bằng nhau.
3. Hai tam giác bằng nhau nếu có hai góc và cạnh kề của tam giác này bằng hai góc và cạnh kề của tam giác kia.
4. Một đường tròn bị chia đôi bởi một đường kính.
5. Góc nội tiếp trong nửa đường tròn là một góc vuông.
Chúng ta được cho biết rằng Thalēs đã sử dụng định lý 3 để tìm khoảng cách từ một con tàu đến bờ biển. Chúng ta không biết chắc phương pháp này là gì, nhưng Hình 3-1 gợi ý một khả năng. Giả sử rằng con tàu đang ở điểm S, và người quan sát trên bờ đang ở điểm W. Khoảng cách cần biết là SW. Người quan sát đi một quãng đường thích hợp, WM, dọc theo bờ biển vuông góc với SW, và cắm một cây gậy trên cát tại M. Anh ta tiếp tục đi theo cùng hướng một quãng đường MP bằng WM. Bây giờ anh ta ở điểm P. Cuối cùng, anh ta đi vào đất liền, theo đường vuông góc với WP, cho đến khi anh ta nhìn thấy con tàu ở S, và cây gậy ở M trên một đường thẳng. Khi đó anh ta đang ở Q, và PQ là khoảng cách cần biết, có thể đo được.
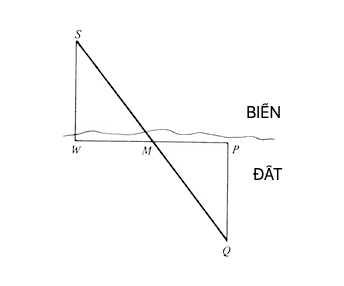
Hình 1
Theo Proclus, Thalēs đã mang hình học từ Ai Cập vào Hy Lạp, và tự mình chứng minh Định lý 4. Mặt khác, người ta nói rằng Thalēs đã phát hiện ra Định lý 2, nhưng không chứng minh nó.
Làm thế nào Thalēs có thể đưa ra những bằng chứng như trên? Thật khó mà tin rằng ông — người đầu tiên suy nghĩ theo hướng này — đã bắt đầu ngay với những ý tưởng và tiên đề cơ bản, giống như chúng ta. Nếu không có một tập hợp các tiên đề để bắt đầu, thì những chứng minh của ông phải mang tính chất trực giác, chứ không phải là bằng chứng theo nghĩa hiện đại. Ví dụ, Thalēs có thể đã chứng minh Định lý 4 bằng cách gấp một hình tròn dọc theo một đường kính.
Có những điểm khác biệt quan trọng giữa hình học của Thalēs với hình học của người Ai Cập và người Babylon. Thalēs là người đầu tiên xây dựng các thuộc tính của những hình thể dưới dạng các mệnh đề tổng quát. Người Ai Cập và người Babylon đã không nghĩ đến việc đề cập tới chúng một cách minh thị. Có vẻ như Thalēs đã quan tâm đến tự thân các hình dạng hình học, và có lẽ ông còn cảm thấy nhu cầu đặt, ngay cả những đặc tính hiện ra như hiển nhiên, trên loại luận cứ lô-gic. Hơn nữa, những đặc tính mà ông thấy lý thú có tính chất khác với những đặc tính mà người Babylon và người Ai Cập từng quan tâm; những vấn đề họ đặt ra luôn luôn liên quan đến việc tính toán một chuyện gì đó (mặc dù, với người Babylon, không phải lúc nào họ cũng tính toán về những vấn đề thực tiễn). Nghĩa là mặt khác, quan tâm của Thalēs hướng tới loại tính chất hình học của các hình thể.
Lucas N. H. Bunt, Phillip S. Jones, Jack D. Bedient,
Thales and His Importance to Mathematics
(In: The Historical Roots of Elementary Mathematics,
Englewood Cliffs, N.J. : Prentice-Hall, 1976,
Ch. 3.3, tr. 69-71)
