DẪN VÀO LÔ-GIC HỌC KÝ HIỆU
(1960)

Tác giả: A. H. Basson & D. J. O’Connor
Người dịch: Nguyễn Văn Khoa

*

1 – Từ Lô-gic học cổ điển đến Lô-gic học ký hiệu[1].

Lô-gic học ký hiệu có một lịch sử ngắn và lô-gic học truyền thống hay cổ điển của Aristotelēs có một lịch sử dài[2]. Tuy nhiên, sự khác nhau giữa chúng chỉ là sự khác biệt của các giai đoạn phát triển khác nhau. Liên quan giữa lô-gic học cổ điển với lô-gic học ký hiệu chỉ như giữa cái phôi với sinh vật trưởng thành. Cần phải nhấn mạnh trên điểm này ngay từ đầu, vì đã có một số tranh cãi nhất định về bản chất và vị thế của lô-gic học ký hiệu, đặc biệt là trong suốt 50 năm qua. Được đào tạo về lô-gic học cổ điển, các nhà lô-gic triết học đôi khi phê phán công việc của các nhà lô-gic học biểu tượng trên cơ sở cho rằng nó bao hàm những quan niệm sai lầm về bản chất của lô-gic học. Ngược lại, các nhà lô-gic học biểu tượng đôi khi phê phán những khiếm khuyết của lô-gic học truyền thống như thể nó đã hoàn toàn lỗi thời.

Hiện nay các nhà lô-gic học đều đồng ý rằng lô-gic học ký hiệu hiện đại là sự phát triển của các khái niệm và kỹ thuật tiềm ẩn trong trước tác của Aristotelēs. Nhưng sự thật này đã bị che khuất trong một thời gian dài, bởi lịch sử lạ lùng của chủ đề. Nền tảng của lô-gic học đã được Aristotelēs đặt ra một cách xuất sắc và hoàn bị từ thế kỷ thứ IV tCn, tới mức là đối với hầu hết những người kế thừa ông, nó hầu như là một môn khoa học hoàn chỉnh. Bây giờ người ta nhận ra rằng cách xử lý của ông chỉ đề cập tới một nhánh lô-gic học nhỏ (mặc dù quan trọng). Hơn nữa, nguyên nhân của sự thành tựu xuyên suốt của ông một phần là do sự thất bại của các nhà lô-gic học: họ đã không thể đưa ra một đóng góp đáng kể nào cho chủ đề này suốt hai nghìn năm sau.

Các nghiên cứu gần đây về lịch sử lô-gic học đều chỉ ra rằng cả những người kế thừa Aristotelēs ở Hy Lạp và các học giả thời Trung Cổ đều đã thực hiện một số khám phá lô-gic học quan trọng. Nhưng tầm quan trọng của các khám phá này thường không được nhận ra vào thời điểm chúng được phát hiện, và do đó đã không khởi đầu được bất kỳ một giai đoạn hồi sinh nào trong sự phát triển của lý thuyết và kỹ thuật lô-gic học. Thất bại này có hai lý do. Sự tin tưởng chung rằng mọi khám phá lô-gic học quan trọng đều đã được Aristotelēs thực hiện có xu hướng ngăn cản các triết gia đánh giá bất kỳ khám phá mới nào ở mức giá trị thực sự của nó. Nhưng lý do thứ hai và quan trọng hơn là tình trạng kém phát triển của khoa toán học trước thế kỷ XVII.

Aristotelēs đã đưa vào lô-gic học khái niệm quan trọng về biến tố (variable). Ý niệm này nay đã trở thành hoàn toàn quen thuộc với mọi người học thức, vì dù là nam hay nữ, họ đều đã từng gặp nó trong lớp khi được dạy đại số học  sơ cấp. Biến là một ký hiệu có thể đại diện cho bất kỳ giá trị nào trong một phạm vi giá trị nào đấy. Do đó, nếu x² = 4 và x là một biến nằm trong phạm vi số thực thì phương trình chỉ đúng với hai giá trị của biến, nghĩa là khi x nhận một trong hai giá trị + 2 hoặc - 2. Việc sử dụng biến trong toán học sơ cấp đã quá quen thuộc để còn cần bình luận. Nhưng nó đã trở nên quen thuộc thông qua sự phát triển và phổ biến tri thức toán học. Sự sử dụng các biến trong lô-gic học của Aristotelēs chỉ giới hạn vào việc biểu thị những hạn từ được sử dụng trong tam đoạn luận bằng các chữ cái trong bảng chữ cái, nhằm làm rõ hơn cấu trúc lô-gic học của các lập luận thuộc loại hình này. Nhưng sự sử dụng các biến trong lô-gic học ký hiệu rộng hơn thế nhiều. Và đây cũng không phải là cách duy nhất mà sự phát triển của toán học đã góp phần vào sự hồi sinh của lô-gic học. 

Một nhà lô-gic học học hiện đại nổi tiếng — [Clarence Irving Lewis[3]...] — đã trích dẫn ba đặc điểm của lô-gic học biểu tượng như sau:

(1) Việc sử dụng các ký hiệu ghi ý (ideograms) hay dấu hiệu đứng thay trực tiếp cho các khái niệm, thay vì các ký hiệu ghi âm (phonograms) hay dấu hiệu đứng thay trực tiếp cho các âm thanh và chỉ gián tiếp cho các khái niệm. Ví dụ: dấu nhân (x) hoặc dấu chấm hỏi (?) là các ký hiệu ghi ý, cũng như các ký tự viết của tiếng Trung Hoa. Nhưng các từ viết «dấu nhân» hoặc «dấu hỏi» trực tiếp đại diện cho các từ nói tiếng Việt tương ứng với chúng, cũng như những từ trong mọi ngôn ngữ được viết theo một số quy tắc ngữ âm.

(2) Phương pháp diễn dịch. Đây là điều ta đã quen thuộc với môn hình học ở trường. Đặc điểm của phương pháp này là từ một số lượng nhỏ các phát biểu, chúng ta có thể tạo ra, bằng cách áp dụng một số lượng hạn chế các quy tắc, một số lượng không xác định những phát biểu khác, thường là mới và đáng ngạc nhiên.

(3) Việc sử dụng các biến có phạm vi ý nghĩa xác định. (Điểm này đã được đề cập rồi.)

Ba đặc điểm này của lô-gic học ký hiệu cũng hiển nhiên là những đặc điểm của toán học. Do đó, sự phát triển của lô-gic học ký hiệu gắn liền với sự phát triển của toán học, và điều quan trọng là tất cả những người tiên phong trong lĩnh vực này đều là các nhà toán học, hoặc triết gia được đào tạo về các phương pháp toán học và biết đánh giá cao chúng.

Cái tên quan trọng đầu tiên trong quá trình phát triển lô-gic học từ dạng cổ điển truyền thống sang dạng ký hiệu hiện đại là G. W. von Leibniz (1646-1716)*. Ông được tôn vinh vừa như triết gia vừa như nhà toán học, được biết tới nhiều nhất trong tư cách là người đồng phát minh ra phép tính vi phân với Newton. Trước tuổi hai mươi, ông đã xuất bản một quyển sách tựa đề là Dissertatio de Arte Combinatoria, trong đó ông đưa ra một kế hoạch cải cách lô-gic học gồm có hai phần. Đầu tiên ông đề nghị thiết lập một ngôn ngữ khoa học phổ quát (characteristica universalis) trong đó mọi khái niệm khoa học đều có thể được biểu đạt bằng sự kết hợp những ký hiệu tượng hình cơ bản. Ngoài đề nghị thay thế những chữ ghi âm bằng những chữ tượng hình, đề xuất này thuộc về ngôn ngữ học hơn là lô-gic học. Nhưng đề xuất thứ hai của ông quan trọng hơn. Ông gợi ý rằng ta có thể thiết kế một phép tính lý luận phổ quát (calculus ratiocinator) nhằm cung cấp một phương pháp tự động để giải quyết mọi vấn đề có thể được diễn đạt bằng ngôn ngữ phổ quát[4]. Nếu thực hiện xong đề xuất của mình, ông đã cung cấp được một hệ thống lô-gic học biểu tượng. Nhưng kế hoạch của ông vẫn chỉ là một gợi ý chưa được triển khai.

Cái tên quan trọng tiếp theo trong sự phát triển của lô-gic học ký hiệu là George Boole (1815-1864)*. Boole là một nhà toán học từng giữ ghế giáo sư toán học tại Queen's College, Cork. Đóng góp của ông bao gồm việc xây dựng một hệ thống đại số, trong đó các biến đứng thay cho những tập hợp, và các phép tính «nhân» và «cộng» thể hiện các cách kết hợp những tập hợp khác nhau nhằm tạo ra những tập hợp tiếp theo. [...] Boole trình bày hệ thống này lần đầu tiên trong một quyển sách nhỏ mang tựa đề Phân Tích Toán Học Về Lô-gic xuất bản năm 1847, và trong tác phẩm Các Quy Luật Của Tư Duy tiếp theo, ông đã áp dụng thứ đại số của mình vào nhiều nhánh của lô-gic học bao gồm tam đoạn luận của lô-gic học cổ điển. Đây là một bước tiến quan trọng, ở chỗ ông đã chỉ ra rằng học thuyết tam đoạn luận của Aristotelēs — trên thực tế vẫn được cho là có phạm vi rộng trùng hợp với lô-gic học diễn dịch — có thể được chứng minh chỉ là một trường hợp đặc biệt của một loại đại số học lô-gic. Để rồi chẳng bao lâu sau, đến lượt những người kế tục Boole cũng chứng minh rằng đại số học của Boole cũng chỉ là một trong các phép tính ký hiệu cấu thành khoa lô-gic học.

Một đóng góp quan trọng khác của các nhà lô-gic học thế kỷ XIX là công trình của Augustus de Morgan[5] về lô-gic học tương quan (logic of relations) và của William S. Jevons[6], người đã đơn giản hóa và phát triển đại số học của Boole về các tập hợp. Nhưng cái tên quan trọng nhất là một người Mỹ, Charles S. Peirce (1839-1914)*, kẻ đã có những đóng góp sâu rộng cho hầu hết mọi nhánh của lô-gic học, trong một loạt bài báo dài phần lớn chưa xuất bản. Tầm quan trọng của thành tựu ông đạt tới chỉ được nhận thức trong thế kỷ XX, khi trước tác của ông được in ra trong nhiều tuyển tập.

Trong khi đó, trên lục địa Châu Âu, một số nhà toán học cũng quan tâm đến nền tảng của toán học. Công trình của họ, đặc biệt là của Gottlob Frege* và Guiseppe Peano*, được tiếp tục bởi Bertrand Russell. Năm 1910, cộng tác với Alfred N. Whitehead*, ông xuất bản quyển Principia Mathematica*, một tác phẩm đồ sộ trong đó một hệ thống lô-gic học ký hiệu được xây dựng và xây dựng để làm nền tảng cho toàn bộ khoa toán học. Hệ thống lô-gic học ký hiệu hoặc toán học do Russell và Whitehead đưa ra đã thể hiện và củng cố công trình của những người đi trước họ và công bố trước công chúng một báo cáo về sự lột xác của lô-gic học đã diễn ra trong thế kỷ XIX. Từ khi quyển Principia Mathematica được xuất bản, lô-gic học đã trở thành một ngành khoa học phát triển mạnh mẽ.

Như vậy, sự phát triển chậm chạp và hầu như không được chú ý của lô-gic học từ thời Leibniz đã lên đến đỉnh điểm trong một công trình có đối tượng chính là toán học. Nhưng tất nhiên, lô-gic học ký hiệu không chỉ quan trọng cho những nghiên cứu về nền tảng của toán học, mặc dù đây là một lĩnh vực nó có thể hữu ích. Nó chia sẻ với lô-gic học truyền thống chức năng cung cấp một phương pháp kiểm tra tính hợp lệ của các lập luận trong ngôn ngữ thông thường, và thực ra nó còn cho ta nhiều phương pháp quyết định tính hợp lệ hay không của các loại lập luận mà lô-gic học cổ điển không thể kiểm tra được. Đi xa hơn nữa, nó còn cung cấp một thủ tục nhằm phân tích cấu trúc của các mệnh đề[7].  Điều này thường là thuận tiện và đôi khi là cần thiết trong lập luận triết học, nơi mà sự không hoàn hảo và mơ hồ trong cách diễn đạt hàng ngày có xu hướng che khuất ý nghĩa của những phát biểu của chúng ta. Trên thực tế, như ta có thể trông đợi, nếu lô-gic học ký hiệu là một dạng phát triển của lô-gic học cổ điển, thì nó sẽ thực hiện mọi nhiệm vụ mà lô-gic học cổ điển đã làm, và nhiều nhiệm vụ khác nữa mà lô-gic học cổ điển không có khả năng thực hiện.

2 - Việc sử dụng ký hiệu

Một trong những chức năng của lô-gic học cơ bản là cung cấp các phương pháp nhằm kiểm tra tính hợp lệ của lập luận. Để làm việc này, chúng ta phải có khả năng đặt những luận cứ vào các loại khác nhau, sao cho mỗi mẫu của một loại hình nào đấy đều có những đặc điểm chung nhất định với các mẫu khác cùng loại. Những đặc trưng mà các luận cứ có chung theo cách này được gọi là các hình thức lô-gic* của luận cứ. Chúng ta sẽ thảo luận về hình thức lô-gic* trong phần tiếp theo, nên không cần phải nói gì thêm về nó ở đây. Nhưng cái phương pháp truyền thống để phân loại các lập luận do Aristotelēs lần đầu tiên phát minh ra lại liên quan tới việc sử dụng những ký hiệu. Ví dụ, hãy xét hai cặp luận cứ sau:

(1) Không có xã hội tư bản nào là ổn định và một số xã hội tư bản là dân chủ; do đó một số nền dân chủ là không ổn định.

(2) Không có người da đen nào là Giáo hoàng và một số người da đen là người Hồi giáo; do đó một số người Hồi giáo không là Giáo hoàng.

(3) Nếu giá vàng tăng, thì nhập khẩu sẽ tăng. Nhưng nhập khẩu sẽ không tăng. Vì thế giá vàng sẽ không tăng.

(4) Nếu thung lũng được hình thành do sự đóng băng, thì ở đấy sẽ có những tảng đá mòn. Nhưng không có tảng đá mòn nào được tìm thấy ở đấy. Vì vậy thung lũng không phải do sự đóng băng tạo ra.

Nếu ta xem xét các luận cứ này, chúng ta dễ dàng nhận thấy rằng: (a) chúng là hợp lệ (valid = có giá trị); và (b) có những điểm tương đồng giữa (1) với (2) và giữa (3) với (4). Mặt khác, những điểm giống nhau này không nằm trong chủ đề của luận cứ. Vì đề tài của (1) không liên quan gì tới đề tài của (2). Đề tài của (3) cũng không liên quan gì đến đề tài của (4). Nhưng nếu chúng ta thay thế ba hạn từ* trong luận cứ (1) và (2) bằng các chữ cái A, B và C thì sự giống nhau giữa chúng sẽ lộ ra rất rõ ràng. Vì cả (1) và (2) bây giờ trở thành:

(5) Không có A nào là B và một số A là C; do đó một số C không là B.

Tương tự, nếu ta thay thế các mệnh đề cấu thành của (3) và (4) bằng các chữ cái p và q, chúng ta có:

(6) Nếu p thì q. Nhưng không-q. Vì vậy, không-p.

Như vậy, việc sử dụng những ký hiệu (trong trường hợp này là các chữ cái trong bảng chữ cái) cho phép ta làm nổi bật các đặc điểm có tầm quan trọng lô-gic trong những luận cứ, và do đó phân chúng ra thành các loại, ở đấy chúng ta có thể áp dụng các quy tắc tổng quát.

Các ký hiệu được sử dụng trong những ví dụ nêu trên là các biến, vì chúng có thể đại diện cho bất kỳ hạn từ* nào trong trường hợp này, hoặc bất kỳ phát biểu nào trong trường hợp kia. Việc sử dụng các biến trong lô-gic học cho phép ta nêu các quy tắc tổng quát nhằm kiểm tra tính hợp lệ của những luận cứ. Do đó, chúng ta có thể nói rằng bất kỳ luận cứ nào thuộc loại hình: «nếu không A nào là B và một số A là C, thì một số C không là B», đều là một luận cứ hợp lệ. Và bất kỳ luận cứ nào thuộc loại hình: «Nếu p, thì q: nhưng không-q. Do đó, không p» đều hợp lệ tương tự. Như vậy, một chức năng quan trọng của ký hiệu trong lô-gic học là biểu đạt tính tổng quát của các quy tắc lô-gic học. Nhưng đấy không phải là chức năng duy nhất của chúng. Công dụng thứ hai và hầu như không kém quan trọng của ký hiệu trong lô-gic học là mang lại sự ngắn gọn và tính kinh tế trong sự diễn đạt cho những phát biểu phức tạp, vốn là khó hoặc không thể hiểu được nếu chúng được diễn đạt bằng ngôn ngữ thường ngày. Việc sử dụng ký hiệu này là hiển nhiên trong đại số học cơ bản. Hãy thử xét cặp biểu thức tương đương sau:

(7) Tích của tổng và hiệu của hai con số bằng hiệu của bình phương của hai con số đó.

(8) (a + b) (a - b) = (a² -  b²).

Để nắm bắt được ý nghĩa của (7), ta cần làm một nỗ lực tinh thần nhất định, trong khi (8) là rõ ràng tức thì đối với bất kỳ ai đã quen sử dụng các ký hiệu liên quan. Và khi những biểu đạt còn phức tạp hơn, thì cách phát biểu chúng bằng ngôn ngữ thông thường là quá dài và quá phức tạp để diễn đạt ý nghĩa của chúng một cách rõ ràng. Có thể diễn đạt mà không cần sử dụng các ký hiệu toán học một phát biểu như sau: «các căn của phương trình ax²+bx+c = 0 được cho bởi công thức sau»:   

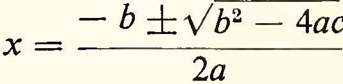
Nhưng cách diễn đạt ngôn ngữ tương ứng sẽ cực kỳ cồng kềnh tới mức rất khó hiểu về mặt tâm lý. Ưu điểm của sự ngắn gọn và trong sáng mà việc sử dụng ký hiệu mang lại cho chúng ta càng trở nên rõ ràng hơn với những loại hình suy luận toán học còn phức tạp hơn nữa. Về mặt lý thuyết, có lẽ ta có thể diễn đạt bất kỳ công thức toán học hoặc phép tính nào bằng ngôn ngữ hàng ngày mà không cần đến sự trợ giúp của một hệ thống ký hiệu đặc biệt. Thế nhưng, nếu cố gắng làm điều này, chúng ta sẽ sớm đạt tới giới hạn của khả năng hiểu được trong thực tế. Để hiểu các biểu thức toán học và làm việc với chúng, ta cần một hệ thống ký hiệu đặc biệt. Và điều này cũng đúng với lô-gic học, một khi chúng ta vượt qua mức độ đơn giản nhất của nó.

Đây không phải là những lợi điểm duy nhất của lô-gic học ký hiệu. Mỗi ngành khoa học đều có những từ kỹ thuật đặc biệt nhằm diễn tả những khái niệm riêng biệt của môn học đó. Và những thuật từ toán học và lô-gic học này thường được biểu trưng một cách thuận tiện nhất bằng loại ký hiệu tượng hình đặc biệt. Ví dụ nổi tiếng nhất về một khái niệm mới, được biểu trưng bằng chữ tượng hình đặc biệt là dấu 0 trong số học. Trong ký hiệu số học của Hy Lạp và La Mã không có bất kỳ ký hiệu nào cho số «không», và do đó, các con tính số học đơn giản như «6032 x 54» hoặc «2425 chia cho 25», mà ngày nay một cậu học sinh 10 tuổi có thể thực hiện, đòi hỏi một khả năng toán học đáng kể và một lượng lao động khổng lồ. Và chúng ta chỉ cần nghĩ xem sự tính toán sẽ như thế nào, nếu chúng ta thiếu các dấu hiệu đặc biệt như dấu nhân và dấu cộng, thiếu chỉ số, dấu tích phân và những thứ tương tự, để thấy tầm quan trọng của loại chữ tượng hình đặc biệt nhằm biểu diễn các phép tính. Trong lô-gic học, chúng ta cũng sẽ cần có những ký hiệu để biểu diễn các phép toán lô-gic, ngoài những biến được đề cập ở trên.

3 - Hình thức lô-gic[8]

Chúng ta đã nói đủ về việc sử dụng ký hiệu trong lô-gic học, và cho thấy rằng có một ngôn ngữ ký hiệu để có thể dịch sang đấy những tài liệu lô-gic học ta phải xử lý không chỉ đơn thuần là một yêu cầu có tính mô phạm. Ngược lại, để hiểu và phát triển khoa lô-gic, có một ngôn ngữ ký hiệu là điều thiết yếu. Bây giờ chúng ta phải quay lại một đề tài rất quan trọng đã được đề cập ngắn gọn ở phần trước: vấn đề hình thức lô-gic.

Sự phân biệt giữa cái chất liệu làm nên một vật, và cái hình thức, hình dạng hoặc cách tổ chức của nó là sự một phân biệt đã quen thuộc với lẽ thường. Nhà điêu khắc có thể tạo hình một bức tượng bán thân bằng đất sét, đá cẩm thạch, gỗ hoặc bất kỳ một chất dẻo nào khác. Hình thức mà ông ta áp đặt lên vật liệu của mình trong mỗi trường hợp đều giống nhau, nhưng chất liệu lại khác nhau. Ngược lại, cùng một chất liệu có thể được nặn thành hay có thể mang nhiều hình dạng khác nhau. Một thỏi chì có thể được đúc theo ý muốn của ta dưới tác động của nhiệt và sức ép. Và nước có thể chuyển thành nước đá hoặc thành hơi nước khi thay đổi nhiệt độ. Khái niệm về hình thức lô-gic chỉ đơn thuần là một sự mở rộng, bằng phép loại suy hoặc phép ẩn dụ, của ý niệm thường thức này.

Việc mở rộng ý niệm hình thức hoặc cấu trúc bằng ẩn dụ như vậy còn rất quen thuộc trong nhiều bối cảnh khác. Ta thường nói tới một bản nhạc ở dạng sonata, hoặc một bài thơ ở dạng sonnet; ở đây, ý niệm hình thức đã được mở rộng hay khái quát hóa để áp dụng cho những thứ khác hơn là vật chất. Và ta cũng áp dụng một cách tương tự khái niệm cấu trúc, vốn được sử dụng ban đầu cho những đối tượng vật chất như các tòa nhà hoặc các sinh vật, vào những thực thể không được xem là vật chất, khi chúng ta nói về «cấu trúc xã hội» hay «cấu trúc của vô thức».

Như vậy, ta không hề mở rộng khái niệm quá mức khi nói về hình thức lô-gic hay cấu trúc lô-gic.  Cấu trúc, hình thức hay tổ chức của một sự vật được cấu thành bởi cách thức những bộ phận của nó được ghép lại với nhau, và bởi các quan hệ qua lại giữa những bộ phận. Như vậy, ta có thể nói về hình thức lô-gic của một phát biểu hoặc tập hợp những phát biểu cấu thành một luận cứ, và khi làm như vậy, chúng ta có ý định phân biệt hình thức hay cấu trúc của phát biểu hoặc luận cứ với chủ đề của nó. Do đó, trong các ví dụ (1) và (2) ở đoạn 2 phía trên, các từ «xã hội tư bản», «xã hội ổn định» và «nền dân chủ» một bên, và «người da đen», «Giáo hoàng» và «người Hồi giáo» bên kia, truyền tải chủ đề của luận cứ. Nhưng mệnh đề «Nếu không có A nào là B, và một số A là C, thì một số C không phải là B» cho chúng ta hình thức của luận cứ, chỉ ra quan hệ giữa các bộ phận cấu thành của nó. Trong các chương sau, chúng ta sẽ thấy rằng trong lô-gic học, ta chỉ quan tâm đến hình thức của các luận cứ chứ không hề tới chủ đề của chúng. Đây là một trong các lý do khiến chúng ta có thể loại bỏ những từ đề cập tới chủ đề, và thay thế chúng bằng các biến.

Việc sử dụng ký hiệu trong lô-gic học và hình thức lô-gic là hai chủ đề liên quan chặt chẽ với nhau, như ta sẽ thấy. Trong các giai đoạn sơ đẳng của lô-gic học, một trong các công dụng chính của một hệ thống biểu trưng tốt là sự mổ xẻ và phô bày một cách rõ ràng cái hình thức lô-gic của thứ tài liệu chúng ta đang xử lý. Và một trong các lợi thế của lô-gic học ký hiệu, so với cái hình thức cổ điển kém phát triển hơn của nó, là nó có một kho ký hiệu đầy đủ hơn, nên nó cho phép chúng ta phô bày được các hình thức lô-gic của những luận cứ không có chỗ đứng trong lô-gic học của Aristotelēs. (Ngay cả một luận cứ rất đơn giản như: «Nếu London lớn hơn Paris, và Paris lớn hơn Rome, thì London lớn hơn Rome», cũng không thể được hấp thu vào các hình thức chuẩn của lô-gic học cổ điển.)

Nhưng vì sao các nhà lô-gic học lại quan tâm đến hình thức lô-gic? Câu trả lời là: bởi vì giá trị của các luận cứ phụ thuộc vào hình thức lô-gic của chúng, và vì với tư cách là nhà lô-gic học, ta quan tâm đến tính hợp lệ (của lập luận). Thoạt nhìn, đây có vẻ là một câu trả lời đáng ngạc nhiên. Ta có thể nghĩ rằng khi nhà lô-gic học suy luận và tranh luận chỉ để đạt tới những kết luận đúng, thì quan tâm chính của họ phải là chân lý hơn là tính hợp lệ. Nhưng khi suy nghĩ kỹ, rõ ràng là ta cần có hai điều kiện để đảm bảo tính đúng đắn của kết luận trong bất kỳ một mảnh lý luận nào. Đầu tiên, bằng chứng hoặc tiền đề từ đấy chúng ta đưa ra suy diễn của mình phải đúng sự thật. Và thứ hai, bản thân những suy diễn cũng phải đúng hoặc hợp lệ. Trong hai điều kiện trên, lô-gic học chỉ có thể đảm bảo điều kiện thứ hai. Sự thật của các mệnh đề trên, vốn không thể suy diễn một cách hình thức từ các mệnh đề khác, phải được thiết lập bằng những phương tiện nằm ngoài phạm vi của lô-gic học hình thức. Và để khỏi có  ai phải nghĩ rằng điều đáng ngạc nhiên là vấn đề chân lý có thể được tách rời vấn đề giá trị theo cách này, cần nhấn mạnh rằng trên thực tế có rất ít liên hệ giữa hai vấn đề trên.

Rõ ràng là trong trường hợp lập luận không hợp lệ, không có liên hệ thiết yếu nào giữa tính đúng hoặc sai của các tiền đề với tính đúng hoặc sai của kết luận rút ra từ các tiền đề ấy. Các tiền đề và kết luận có thể phô bày bất kỳ kết hợp nào trong bốn cái có thể xảy ra:  đúng, đúng; đúng, sai; sai, đúng; và sai, sai. Đấy là lý do khiến các luận cứ không hợp lệ là vô dụng hoặc khỏi quan tâm. Nhưng thoạt nhìn, trường hợp của những lập luận hợp lệ cũng không quá khác biệt. Trong bốn kết hợp có thể có giữa cái đúng hoặc cái sai của các tiền đề và kết luận, chỉ có một trường hợp là không thể xảy ra, đấy là trường hợp các tiền đề là đúng mà kết luận là sai. Bất kỳ kết hợp nào khác trong ba cái còn lại đều có thể xảy ra. Có vẻ như chúng ta khó có thể lập luận từ các tiền đề sai đến một kết luận đúng một cách hợp lệ. Nhưng luận cứ sau đây rõ ràng là một lập luận hợp lệ:

Tất cả các hoàng đế La Mã đều là tổng thống của Hoa Kỳ

Lincoln là một hoàng đế La Mã.

Do đó, Lincoln là tổng thống của Hoa Kỳ.

Kết luận trên là đúng, bất chấp cái sai của cả hai tiền đề lẫn tính hợp lệ của lập luận.

Trên thực tế, bảo đảm duy nhất do tính hợp lệ của một lập luận mang lại chỉ là điều này: nếu các tiền đề của một luận cứ hợp lệ là đúng, thì kết luận chắc chắn cũng là đúng. Nhưng khi các tiền đề là không đúng, thì chúng ta không biết kết luận là đúng hoặc sai, ngay cả khi ta được đảm bảo rằng lập luận ấy là hợp lệ. Như vậy, lô-gic học không quan tâm trực tiếp đến tính chân lý về mặt sự kiện của các phát biểu, kể cả khi những phát biểu đó là tiền đề hoặc kết luận của các luận cứ. Và nó chỉ liên quan đến sự thật một cách gián tiếp, trong chừng mực nó là hệ quả của giá trị (tính hợp lệ) của một luận cứ mà chúng ta có thể thừa nhận cái đúng của kết luận do cái đúng của các tiền đề[9].

Do đó, trong các chương tiếp theo, chúng ta sẽ quan tâm đến những phương pháp kiểm tra tính hợp lệ của các hình thức lập luận khác nhau. Các phương pháp này đòi hỏi ta phải chú ý tới cấu trúc lô-gic hay hình thức lô-gic của những lập luận, bởi vì tính hợp lệ của một luận cứ phụ thuộc vào một số đặc điểm nhất định nơi hình thức lô-gic của nó. Và để bỏ qua chủ đề của các lập luận mà chỉ chú ý đến hình thức lô-gic của chúng thôi, thì điều rất thuận tiện là ta cứ luôn luôn biểu thị mọi luận cứ thuộc một dạng nhất định nào đấy, bằng một ký hiệu biểu trưng thích hợp, sao cho những đặc trưng cấu trúc hữu quan của nó có thể được làm rõ ra và thử nghiệm. Tất cả những điều nói trên đều liên quan đến sự áp dụng thực tiễn của lô-gic học ký hiệu. Nhưng giống như bất kỳ một ngành khoa học nào khác, lô-gic học đã không hề được nghiên cứu trước tiên vì lý do tiện ích. Sự phát triển của các kỹ thuật lô-gic học vượt xa những gì là cần thiết nhằm cung cấp một phương pháp kiểm tra tính hợp lệ hay không cho các hình thức lý luận; nó là một công việc được thực hiện vì và cho chính bản thân nó, giống như sự phát triển của toán học thuần túy. Có nhiều ngành toán học vẫn chưa có ứng dụng thực tiễn nào được phát hiện cho các vấn đề thuộc thuật kỹ sư, khoa học tự nhiên hoặc thống kê. Điều này cũng đúng cho khoa lô-gic học ký hiệu còn non trẻ. Tuy nhiên, ngay cả ở đây, nhiều nhánh của lô-gic học, lúc đầu được triển khai vì sự hấp dẫn nội tại của chúng, đã được phát hiện là có thể hữu dụng và có những ứng dụng thực tiễn trong các lĩnh vực khó tin có thể xảy ra nhất — từ việc chế tạo máy tính đến việc lập trình các mạch điện. Trong quyển sách này, chúng ta sẽ quan tâm đến những phần cơ bản hơn, và theo truyền thống, mang tính thực tiễn hơn của chủ đề. Dù sao, cần phải nhớ rằng lô-gic học hiện nay là một môn học đang phát triển nhanh chóng, rằng có nhiều lĩnh vực tri thức rộng lớn và hầu như chưa được khám phá còn nằm ngoài biên giới hiện tại của nó.

4 - Suy diễn (Inference) và bao hàm (Implication).

Trong Phần 2 ở trên, chúng ta đã xem xét một số ví dụ về các lập luận hình thức đơn giản nhằm giới thiệu khái niệm hình thức lô-gic. Và đã lấy  ví dụ (1), được trình bày như sau:

(1) Không có xã hội tư bản nào là ổn định và một số xã hội tư bản là nền dân chủ; do đó, một số nền dân chủ là không ổn định.

Chúng ta cũng có thể tự biểu đạt như sau:

(la) Nếu không có xã hội tư bản nào là ổn định và một số xã hội tư bản là nền dân chủ; thì một số nền dân chủ là không ổn định.

Nhưng có một khác biệt giữa (1) và (1a), và khác biệt này là quan trọng. Một mặt, (la) là một tuyên bố lô-gic có tác dụng rằng nếu một số điều kiện nhất định được đáp ứng, thì một số hậu quả nhất định sẽ xảy ra. Nó không nói gì về việc liệu các điều kiện được đề cập trong mệnh đề-nếu (if-clause) có được đáp ứng trên thực tế hay không. Mặt kia, (1) là hoàn toàn khác. Trong các tiền đề của (1), một số khẳng định nhất định được đưa ra, và như một hệ quả lô-gic của các khẳng định này, một khẳng định khác nữa được đưa ra, cụ thể là cái sự kiện được nêu ra trong kết luận. Vì vậy, để có thể biện minh cho khẳng định (1), chúng ta không chỉ phải biết rằng hình thức lô-gic của lập luận đảm bảo rằng cái kết luận sẽ tuân theo các tiền đề, mà còn phải biết rằng các tiền đề ấy là đúng. Và, như chúng ta đã thấy, điều kiện cuối cùng này không liên quan gì tới vấn đề lô-gic về tính hợp lệ. Mặt khác, chúng ta có thể được biện minh khi khẳng định (la) mà không phải có thiên kiến gì về tính đúng hay sai của các tiền đề. Chẳng hạn, nhà đối lập theo chủ nghĩa Mark thô bạo nhất có thể cam kết với (la) một cách an toàn, trong khi anh ta chắc chắn sẽ không cam kết với (1) chẳng hạn. Anh ta có thể cam kết với (la), bởi vì trong trường hợp này anh sẽ chỉ nói: «nếu tiền đề là đúng thì kết luận là đúng» mà thôi.

Để đánh dấu sự khác biệt quan trọng này, người ta thường gọi các lập luận như (1) là suy diễn, và những phát biểu dưới dạng (la) là bao hàm. Khi đưa ra một suy diễn, chúng ta thừa nhận tính đúng đắn của các tiền đề bằng sự khẳng định chúng; và do hậu quả của tính đúng đắn của các tiền đề, cũng như do giá trị lô-gic của lập luận, chúng ta có quyền khẳng định kết luận. Nhưng khi chỉ đưa ra một bao hàm [mệnh đề-nếu], thì chúng ta không qua đó cam kết với sự thật của các tiền đề.

Sẽ là điều hoàn toàn chính xác trong các sách giáo khoa về lô-gic học, nếu chúng ta đặt mọi ví dụ dưới dạng bao hàm, vì ta không quan tâm tới sự thật vật chất của các tiền đề, mà chỉ quan tâm đến giá trị lô-gic của hình thức biểu đạt ta đang sử dụng. Tuy nhiên, có lẽ sự diễn đạt những ví dụ của ta dưới dạng luận cứ, nghĩa là dưới dạng suy diễn là thông thường hơn, vì lập luận hàng ngày của chúng ta, vốn được thiết kế để xác lập tính đúng đắn của kết luận, thường phải được đúc theo khuôn mẫu đó, nên trong quyển sách này, chúng tôi sẽ đưa ra các ví dụ của mình dưới dạng suy diễn nơi nào trình bày như thế là thuận tiện và tự nhiên hơn. Không nhầm lẫn nào có thể xảy ra, miễn là người đọc ghi nhận sự khác biệt giữa suy diễn và bao hàm trong trí nhớ.

A. H. Basson & D. J. O’Connor,
Dẫn Vào Lô-gic Học Ký Hiệu
 (Introduction to Symbolic Logic,
New York: The Free Press, 1960, tr. 1-15).